Introduction
In mathematics and computer science, factorials play a crucial role in various computations and problem-solving techniques. The concept of factorial, denoted by the symbol “!”, is straightforward yet immensely powerful. A factorial of a non-negative integer ( n ) is the product of all positive integers less than or equal to ( n ). This seemingly simple operation finds applications in permutations, combinations, series expansions, and more.
A factorial calculator is a tool designed to simplify the process of calculating factorials, especially for large numbers where manual computation is impractical. This article delves into the significance of factorials, the mechanics behind a factorial calculator, its applications, and the methods used to implement such a tool.
Data Visualization with Matplotlib: A Comprehensive Guide
Understanding Factorials
Definition and Notation
The factorial of a non-negative integer ( n ) is denoted by ( n! ) and is defined as:
[ n! = n \times (n-1) \times (n-2) \times \ldots \times 3 \times 2 \times 1 ]
For instance:
- ( 5! = 5 \times 4 \times 3 \times 2 \times 1 = 120 )
- ( 0! = 1 ) by definition, which serves as a base case in many recursive algorithms.
Historical Context
The concept of factorials dates back to ancient times, with the earliest recorded use by Indian mathematician Pingala around 300 BCE in the context of combinatorial mathematics. Factorials gained prominence in the work of European mathematicians in the 17th and 18th centuries, particularly in the study of permutations and probability.
Properties of Factorials
Factorials exhibit several interesting properties, including:
- Recursive Property: ( n! = n \times (n-1)! )
- Growth Rate: Factorials grow extremely fast. For example, ( 10! = 3,628,800 ), while ( 20! ) is a number with 19 digits.
- Use in Binomial Theorem: Factorials are used in binomial coefficients, which are central to the binomial theorem.
Applications of Factorials
Combinatorics
In combinatorics, factorials are used to count the number of ways to arrange objects. For example, the number of permutations of ( n ) distinct objects is ( n! ). Factorials also appear in formulas for combinations, where the number of ways to choose ( k ) objects from ( n ) objects is given by:
[ \binom{n}{k} = \frac{n!}{k!(n-k)!} ]
Series Expansions
Factorials are essential in the expansions of exponential, trigonometric, and other functions. For example, the Maclaurin series for ( e^x ) is:
[ e^x = \sum_{n=0}^{\infty} \frac{x^n}{n!} ]
Probability and Statistics
In probability theory, factorials are used to calculate probabilities in scenarios involving permutations and combinations. For example, the number of ways to distribute ( n ) identical objects into ( k ) distinct groups involves factorials.
Algorithms and Data Structures
In computer science, factorials are used in algorithms related to sorting, searching, and optimization problems. They also appear in the analysis of algorithm complexity, particularly in problems involving permutations and combinations.
Building a Factorial Calculator
Basic Implementation
A basic factorial calculator can be implemented using a simple loop or a recursive function. Here is a Python example of both methods:
Iterative Method
def factorial_iterative(n):
result = 1
for i in range(1, n + 1):
result *= i
return resultRecursive Method
def factorial_recursive(n):
if n == 0:
return 1
else:
return n * factorial_recursive(n - 1)Handling Large Numbers
Calculating factorials of large numbers can quickly exceed the capabilities of standard data types due to the rapid growth of factorial values. Python handles large integers with its arbitrary-precision int type, but other programming languages may require special libraries or data structures.
Optimizations
Several optimizations can be applied to improve the efficiency of factorial calculations:
- Memoization: Storing previously computed values to avoid redundant calculations.
- Iterative Approaches: Using iteration instead of recursion to prevent stack overflow and reduce overhead.
- Parallel Processing: Dividing the computation into smaller tasks that can be processed concurrently.
Implementing a Factorial Calculator
Below is a more comprehensive Python implementation of a factorial calculator that includes error handling and optimization:
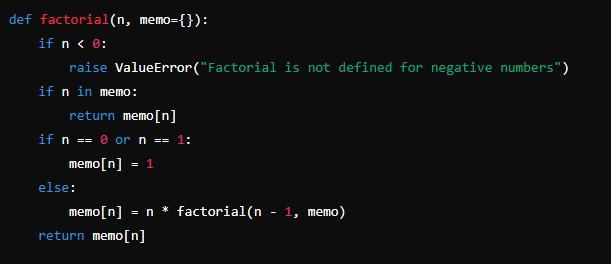
def factorial(n, memo={}):
if n < 0:
raise ValueError("Factorial is not defined for negative numbers")
if n in memo:
return memo[n]
if n == 0 or n == 1:
memo[n] = 1
else:
memo[n] = n * factorial(n - 1, memo)
return memo[n]
# Example usage
try:
number = int(input("Enter a non-negative integer: "))
print(f"The factorial of {number} is {factorial(number)}")
except ValueError as e:
print(e)Applications of Factorial Calculators
Educational Tools
Factorial calculators are valuable educational tools that help students understand the concept of factorials and their applications. They provide immediate feedback, making it easier to explore permutations, combinations, and series expansions.
Scientific Computing
In scientific computing, factorial calculators are used in simulations, probabilistic models, and statistical analyses. They enable researchers to perform complex calculations that would be impractical manually.
Software Development
Software developers use factorial calculators in various applications, including gaming algorithms, optimization problems, and cryptographic functions. Efficient implementations ensure that applications run smoothly, even when dealing with large numbers.
Financial Modeling
Factorial calculators are used in financial modeling to compute probabilities, model risk scenarios, and analyze investment strategies. They help in assessing the likelihood of different outcomes and making informed decisions.
Advanced Topics
Stirling’s Approximation
For very large values of ( n ), calculating ( n! ) directly can be computationally expensive. Stirling’s approximation provides a way to estimate factorials for large ( n ):
[ n! \approx \sqrt{2 \pi n} \left(\frac{n}{e}\right)^n ]
This approximation is useful in scenarios where an exact value is not necessary, but an estimate is sufficient.
Gamma Function
The Gamma function extends the concept of factorials to real and complex numbers. For a positive integer ( n ):
[ \Gamma(n) = (n-1)! ]
The Gamma function is defined as:
[ \Gamma(z) = \int_0^{\infty} t^{z-1} e^{-t} dt ]
It is widely used in advanced mathematics, physics, and engineering.
Computational Complexity
The computational complexity of calculating a factorial is ( O(n) ) for both iterative and recursive methods. However, optimizations such as memoization can improve the practical performance, especially for repeated calculations.
Parallel Computing
In parallel computing, factorial calculations can be distributed across multiple processors to speed up the computation. Techniques such as divide-and-conquer and task parallelism are employed to handle large-scale problems efficiently.
Conclusion
Factorial calculators are indispensable tools in mathematics and computer science. They simplify the computation of factorials, making it feasible to solve problems in combinatorics, probability, and algorithm analysis. Whether used for educational purposes, scientific research, software development, or financial modeling, factorial calculators enhance our ability to perform complex calculations efficiently.
Understanding the principles behind factorials, their properties, and their applications provides a solid foundation for leveraging factorial calculators in various domains. As technology advances, the implementation and optimization of these calculators continue to evolve, further expanding their utility and impact.